首頁【專欄】對稱函數在組合問題中的應用
.jpg)
我們首先看看以下這個中學生也能理解的組合問題：
問1：
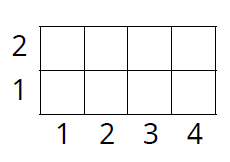
在4×2的方格(如上圖)中填入1…8的數字，並且滿足以下遞增條件：
•若在座標(i,j)的格子填入a，在座標(i+1,j)的格子填入b，則b>a；
•若在座標(i,j)的格子填入a，在座標(i,j+1)的格子填入b，則b>a；
試問有幾種方法？
答1 ：14種，可以如下圖依序枚舉
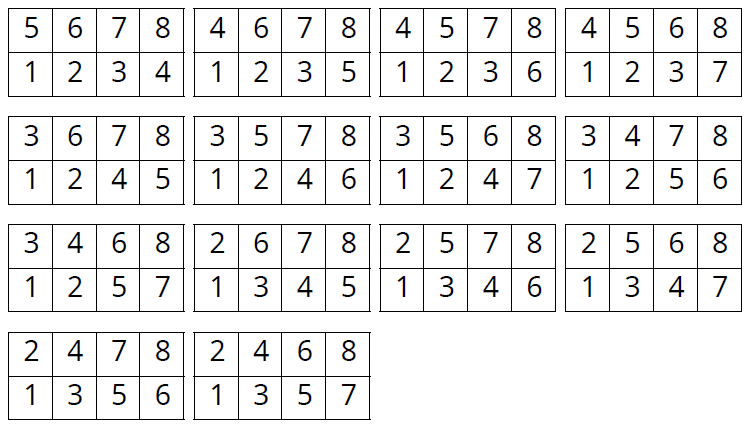
上述的問題可以推廣，4換成任意的正整數n ≥ 0。
問2：
在n×2的方格中填入1…2n的數字，並且滿足以下遞增條件：
•若在座標(i,j)的格子填入a，在座標(i+1,j)的格子填入b，則b>a；
•若在座標(i,j)的格子填入a，在座標(i,j+1)的格子填入b，則b>a；
試問有幾種方法？
答2 : Catalan數
這公式可由遞迴方法證明。現在考慮一個整數1≤m≤n，並考慮以下額外條件：
•座標(m,2)的格子填入2m；
•對所有滿足1≤i
那麼，滿足這二個額外條件的填入數字的方法共有Cm-1Cn-m種。因為每一個填入數字的方法都有一個唯一的m滿足以上額外條件，我們就推得遞迴式
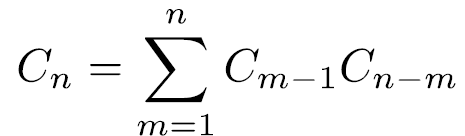
由此遞迴式C0=1以及初始值就可由數學歸納法推得上述對一般n≥0的公式。例如：
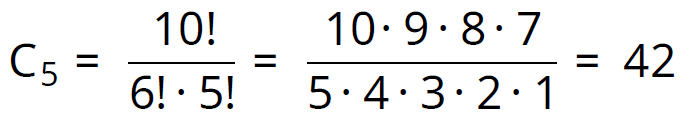
讀者不妨動手驗證5x2的格子真的有42種填入1...10並且滿足遞增條件的方法。
既然n×2的方格有一般的公式(Catalan數)，那這個公式能不能再推廣呢？n×m的方格如何？更不規則的方格圖呢？
問3：
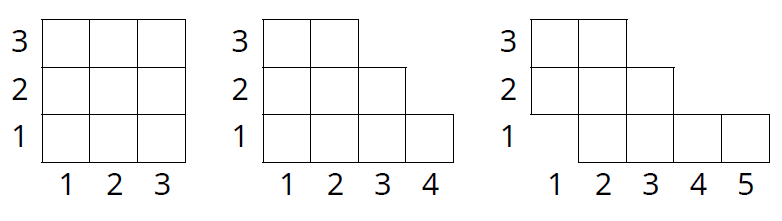
在以上方格圖表中填入1…9的數字，並且滿足以下遞增條件：
•若在座標(i,j)的格子填入a，在座標(i+1,j)的格子填入b，則b>a；
•若在座標(i,j)的格子填入a，在座標(i,j+1)的格子填入b，則b>a；
試問分別有幾種方法？
答3：
分別為84, 168, 450。
前二個數字84, 168可由著名的「鉤長公式」算出，我們現在就來解釋這個公式。
對圖中任一個方格(i,j)定義其鉤長h(i,j) = 正右方與正上方(含自身)方格的總數，例如下圖中：
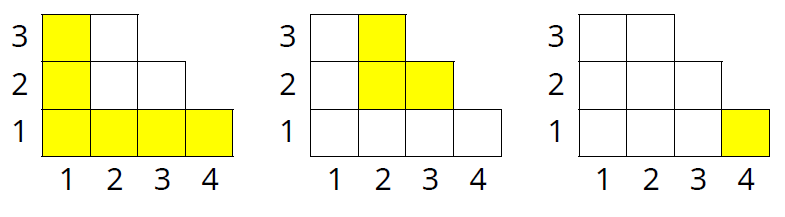
方格(1,1), (2,2), (4,1)的鉤長分別為h(1,1)=6, h(2,2)=3, h(4,1)=1。
如果我們將方格圖各橫列的長度由下而上標示為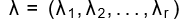
那麼鉤長公式如下：
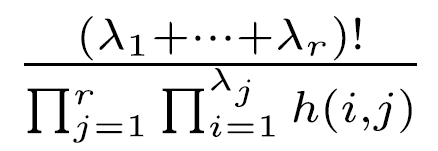
上面的第二個方格圖的橫列長為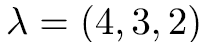 
，所以套用鉤長公式可以算出滿足遞增條件的填表方法數為
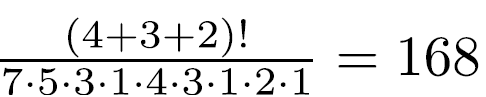
同樣的方法，可以算出3x3的方格共有84種填入1...9，並且滿足遞增條件的方法共有84種。
鉤長公式是1900年由普魯士數學家Ferdinand Georg Frobenius所發現。Frobenius利用排列群Sn的線性表現的特徵函數證明了這個公式，他的方法是現今「對稱函數論」以及「群表現論」二個領域的開端。
「群」是一種數學中用來描述空間對稱性的結構，其中排列群Sn描述的是n個點的集合{1, 2, 3, ..., n}的所有排列（所以Sn有n!個元素）。「群表現」則是描述線性空間(歐式空間)對稱性的代數結構。由於二者的定義會涉及到高等數學，筆者在此就不更深入介紹。
「對稱函數」是一種空間中有對稱性的函數，例如：F(x, y, z) = xy + xz + yz是個對稱函數，這是因為我們可以將x, y, z三個變數任意排列而不影響它的值 ，也就是說：
F(x, y, z) = F(x, z, y) = F(y, x, z) = F(y, z, x) = F(z, x, y) = F(z, y, x)。
我們將這個函數F(x,y,z)稱為「單項式對稱函數」，通常記作m(1,1,0)(x,y,z)。
更一般來說，任意給定一個遞減數列λ = (λ₁≥λ₂≥λ3≥0)，我們都能定義一個對應的單項式對稱函數 mλ，例如：
m(3,0,0)(x,y,z) = x³ + y³ + z³
m(2,1,0)(x,y,z) = x²y + x²z + y²x + y²z + z²x + z²y
m(1,1,1)(x,y,z) = xyz
除了這些單項式對稱函數外，另一組重要的對稱函數稱為Schur函數，記作Sλ，它與對稱群Sn的群表現論息息相關，例如：
s(3,0,0)(x,y,z) = x³ + y³ + z³ + x²y + x²z + y²x + y²z + z²x + z²y + xyz
s(2,1,0)(x,y,z) = x²y + x²z + y²x + y²z + z²x + z²y + 2xyz
s(1,1,1)(x,y,z) = xyz
事實上，Schur函數總是可以寫成單項式對稱函數的倍數的相加：
s(3,0,0) = m(3,0,0) + m(2,1,0) + m(1,1,1)
s(2,1,0) = m(2,1,0) + 2m(1,1,1)
s(1,1,1) = m(1,1,1)
仔細觀察m(1,1,1)這項係數，分別為1, 2, 1，這正好是以下三方格圖中填入1, 2, 3滿足遞增條件的方法數
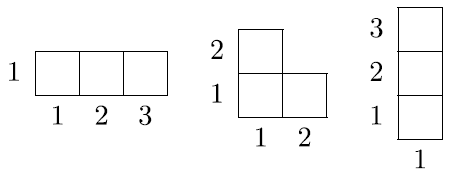
一般來說，如果方格圖橫列長為遞減數列，且一共有n=λ1+…+λr個格子，那麼sλ這個Schur函數中m(1,1,…,1)這項的係數即為在方格圖中填入1, …, n且滿足遞增條件的方法數。
以上解釋的這些係數即是著名的Kostka數，它們在「代數組合論」與「群表現論」中有顯著的地位。20世紀後半以來，「對稱函數論」以及「群表現論」的發展突飛猛進。對稱函數論中，最著名的莫非是英國數學家Ian Grant Macdonald所發現的(q,t)-對稱函數以及(q,t)-Kostka多項式。前者推廣了Schur函數，後者推廣了Kostka數。這二者仍然是現在「群表現論」以及「對稱函數論」中相當熱門的研究主題。
最後，為了展示對稱函數論的應用，我們看看以下問題：
問4:
給定任意一個參數q，將以下x, y, z的對稱函數的乘積展開
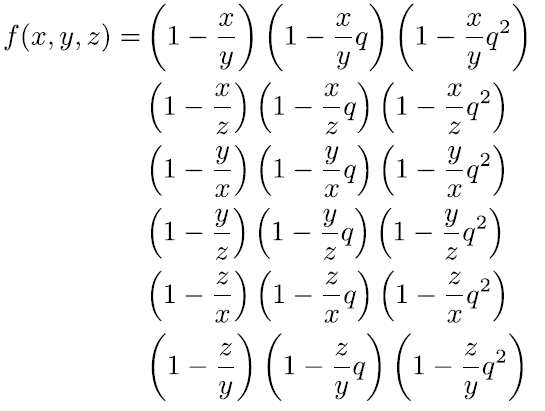
試問常數項(x⁰y⁰z⁰這項)的係數為何？
答4:
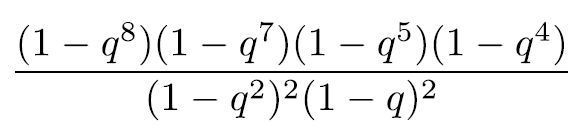
若實際動手計算，這將曠日廢時，畢竟18個二項式的乘積展開將有218 = 262144項。然而，這個答案可以不費吹灰之力，由「Macdonald常數項公式」輕鬆算出。
「Macdonald常數項公式」由俄美數學家Ivan Cherednik於1995年所證明。證明的關鍵是1990年代所發展的「Dunkl算子」以及「雙重仿射Hecke環」這些代數結構的特質，這二個代數結構正是在筆者研究領域的範圍內。
作為結語，現代數學研究中，代數與幾何方法早已隨處可見，許多看似簡而易懂的組合問題背後深藏了代數與幾何的結構。不僅是組合論的研究，在其他數學領域中（例如數論）也是如此。代數領域中的表現論，也因為與各種領域互動接觸，發展出了多采多姿的方法、技術、理論來解決各式各樣的問題。上文所展示的幾個例子不過是窺見一斑。
