【專欄】量子計算與量子模擬:展望與挑戰

在一百年前的1925年,物理學家維爾納.海森堡發展了矩陣量子力學,與後來埃爾文.薛丁格的波函數方程式,一同建構了量子力學的基礎。量子力學進展至今,許多新興領域如量子信息理論、量子計算與量子模擬等,正蓬勃且迅速的更新演化中。因此,聯合國教科文組織宣佈2025年為國際量子科技年,此倡議目的向全球宣傳量子科學與量子科技的重要性,並提升公眾對其潛在應用的可能與展望有更多的認識。
歷經一百年的千錘百鍊,量子力學已被科學界證實其必要性,不管是在解釋粒子物理的標準模型或是研究凝聚態物理的量子材料中,都能藉由量子力學的內涵,即能階量子化、測量的不確定性與機率波等特性,提供有效且精準的描述。近期在冷原子系統中的發展,科學家能有效的控制中性原子或是離子的性質,加上光子的操控與超導位元的進展,這四個主要發展量子科技的平台,相互競爭也相互輝映,在近二十年的演進中,各平台有其擅長的優勢與不易消弭的缺點,大型公司也紛紛成立為要建構實質可用的量子電腦原型,使得在實現量子電腦的競爭中,呈現學界與業界共創榮景的現象,至於哪一個能最先衝破終點線?這個確實不容易回答。但是在這激烈競爭中,可以確定的是量子科學與科技的躍進將會受惠於競爭之下所推展的科研成果。
在這期科普專欄中,我將與大家分享量子科技主要應用的量子計算與量子模擬的展望與挑戰,最後,我簡略的介紹中研院原分所內原子與光學物理組的研究重點,並提出原分所在發展量子科技的藍圖與預期貢獻。
量子計算:0跟1的探戈舞
量子位元 (qubit) 是量子計算的基石,與古典電腦使用的古典位元區別在於量子位元的疊加性質,如果我們使用二進位制的表達式,即0跟1來編碼信息傳遞的方式,那麼古典機器用位元編碼的方式只能是 0 或 1。不同於古典位元,量子位元可以同時處於 0 和 1 的「疊加態」(superposition)。這種特性使量子電腦在處理資訊上具有強大的潛力。然而,量子位元的真正威力來自於「糾纏態」的糾纏性質(entanglement)—當兩個或多個量子位元互相糾纏後,它們的狀態就不再是獨立的,即使相隔遙遠,對其中一個位元的測量結果也會立即影響到其他位元。
量子糾纏的原理可由量子力學的數學描述來理解。假設有兩個量子位元 A 和 B,若它們處於一個糾纏態,用波函數表達就會是 |φ⟩=1/√2(| 00⟩+|11⟩),這表示它們不是個別處於 0 或 1,而是共同處於一種混合疊加的狀態。我們無法單獨描述 A 或 B 的狀態,必須把它們看作一個整體。這種關聯性正是量子計算中能實現指數級並行運算的關鍵。
在量子計算的應用上,疊加性質與糾纏讓量子電腦能同時探索大量可能性。例如,在量子傅立葉轉換(Quantum Fourier Transform)與Shor質因數分解演算法中,糾纏態被用來同時處理多種輸入,並透過量子干涉篩選出正確結果。又如Grover的搜尋演算法,它能在未排序的資料庫中以平方根的時間找到目標,這是傳統演算法無法達到的效率。
總之,量子位元的糾纏態不僅揭示了量子世界的奇特行為,也為人類帶來一種全新的資訊處理方式,開啟了量子計算與量子科技的無限可能。
量子計算:to correct or not to correct, that is the question
量子計算的潛力雖然極大,但也面臨嚴峻挑戰,其中最根本的就是量子錯誤的問題。由於量子位元極其敏感,容易受到外界環境干擾(如:溫度波動、磁場雜訊、或其他系統控制失誤等),導致疊加與糾纏態「退相干(decoherence)」,造成計算錯誤。與傳統電腦不同的是,量子資訊不能被直接複製,所以無法以經典方式備份與修復。因此,必須設計「量子糾錯碼(Quantum Error Correction)」來保護資訊,使量子計算真正可行且可擴展。
量子糾錯碼的核心思想是將一個邏輯量子位元編碼到多個實體量子位元上,透過冗餘與糾纏關係,來檢測與更正錯誤。以中性原子陣列作為量子計算平台,其特點在於可用光鑷(optical tweezers)精確排列上百甚至上千顆中性原子,並以雷射控制其內部能階作為量子位元。這樣的平台具備高度的可擴展性與空間操控性,非常適合實作錯誤修正碼。特別地,中性原子之間可以透過里德堡(Rydberg)態產生強相互作用,使得邏輯閘操作與糾錯流程更有效率。
我們最近就研究使用中性原子的里德堡態實現CZ邏輯閘最佳化的參數空間(圖一),預測此邏輯閘的保真率可達 0.999[1],這提供了目前邏輯閘理論研究與實驗的極限與發展潛力。另外,理論上我們也設計使用原子耦合波導的量子介面製備多位元糾纏的圖態2,也可以提供另一類單向量子計算的途徑。

圖一 (a) 里德堡態與雙光子激發的示意圖。(b) 最佳化雷射激發波形函數。
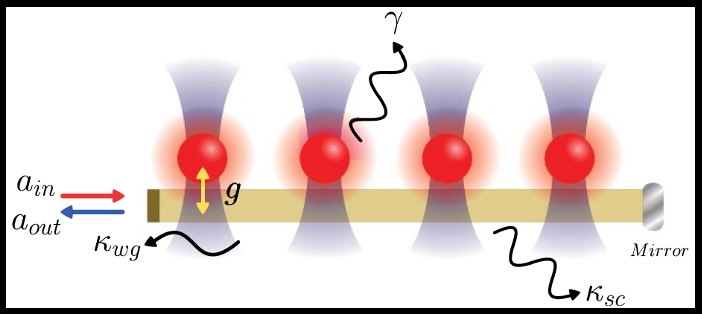
圖二 原子-奈米光子腔示意圖。利用此平台可以使用具有單量子位元閘操作和多量子位元狀態雕刻的電路表達式來編織圖態。
最後,中性原子平台具備重排陣列的能力,可自動填補缺失的位元並重建完美陣列,有助於降低物理錯誤率,進一步提升糾錯效率。這些特性使中性原子陣列成為實現容錯量子計算的有力候選者。所以量子糾錯是讓量子電腦真正可行的關鍵,而中性原子平台正逐步克服實驗挑戰,邁向可容錯的大規模量子計算系統。
量子模擬器
量子模擬是利用可控制的量子系統來模擬其他難以直接研究的量子現象,特別是傳統電腦難以處理的多體量子系統。這項技術分為兩大類:類比量子模擬(analog quantum simulation)與數位量子模擬(digital quantum simulation)。
類比量子模擬是將一個複雜量子系統的哈密頓量「映射」到一個可控制的量子系統上,讓模擬系統自然地演化出欲研究的物理行為。例如,使用光晶格中的冷原子模擬哈伯模型(Hubbard model)來研究高溫超導現象。這種方法在特定模型下非常有效且具有良好的可擴展性,但靈活度較低,只能針對特定問題設計對應系統。
相對地,數位量子模擬則是以量子閘(quantum gates)方式離散地模擬哈密頓量演化。透過邏輯量子位元與量子演算法,可模擬更廣泛的物理現象,並具備容錯與可編程的優勢。這種方法更適合與量子糾錯結合,未來也更有機會在通用量子電腦上實現。然而,它對量子位元的品質與數量要求較高,目前仍在技術突破階段。
目前中性原子、超導電路、離子阱等系統皆被用於實現量子模擬。其中,中性原子因為可排成大規模陣列並具備可調整的相互作用,已成為模擬磁性、自旋液體等量子材料的重要平台。未來的研究願景包括:模擬高能物理中的量子場論、研究非平衡動力學與量子混沌、甚至模擬宇宙早期的量子現象。透過這些模擬,人們希望解答如高溫超導、量子相變、暗能量起源等重大科學問題。然而,量子模擬也面臨挑戰:包括實驗參數精準控制、退相干抑制與系統可擴展性。此外,數位模擬的資源開銷與誤差累積問題仍需解決。
原分所張銘顯與林育如博士最近有使用玻色凝聚態模擬合成方位規範場的工作 [3], 另外詹楊皓與陳應誠博士也在二維方晶格上模擬自旋二分之一的系統 [4],總結來說,量子模擬提供了探討自然界深層結構的嶄新工具,是當代物理與量子科技發展的關鍵方向。隨著硬體與控制技術進步,量子模擬將在基礎研究與未來應用中發揮日益重要的角色。
原分所量子科學與科技的展望
中研院原分所的「原子與光學物理組」聚焦於量子前沿系統,尤其是玻色凝聚態、冷原子、量子光學與量子資訊的實驗與理論研究。該組由6位研究人員與2位合聘研究員(國立臺灣大學藍紹宇副教授與中研院物理所葉崇傑特聘研究員)組成,研究的領域與系統包含 (1)任祥華副與張銘顯副研究員:以冷原子或奈米鑽石中的固態自旋系統為主的量子光學與量子信息科學研究;(2)陳應誠研究員:里德堡原子的量子計算與量子模擬;(3)陳俊嘉助研究員與肖恩助博士:量子感測、連續式光學原子鐘與連續式原子雷射[5];(4)藍紹宇副教授:原子干涉儀與光晶格原子的量子控制;(5) 張銘顯、林育如副研究員與葉崇傑特聘研究員:超冷原子量子氣體的理論與實驗研究,包括超流性、人造規範場、旋量玻色-愛因斯坦凝結等。
我們的研究涵蓋從基本量子現象的探索到量子科技應用的開發,形成一個多元而互補的學術社群。整體而言,原子與光學物理組致力於打造一個理論與實驗並進的研究環境,不僅探索自然界的深層量子機制,也在積極拓展未來量子科技的可能性,為量子感測、模擬與計算奠定基礎,期望在全球量子科技浪潮中扮演關鍵角色。
[1] T. H. Chang, T. N. Wang, H. H. Jen, and Y.-C. Chen, “High-fidelity Rydberg controlled-Z gates with optimal pulses”, New J. Phys. 25, 123007 (2023).
[2] C.-H. Chien, S. Goswami, C.-C. Wu, W.-S. Hiew, Y.-C. Chen, and H. H. Jen, “Generating graph states in an atom-nanophotonic interface”, Quantum Sci. Technol. 9, 025020 (2024).
[3] P.-K. Chen, L.-R. Liu, M.-J, Tsai, N.-C. Chiu, Y. Kawaguchi, S.-K. Yip, M.-S. Chang and Y.-J. Lin, Rotating atomic quantum gases with light-induced azimuthal gauge potentials and the observation of Hess-Fairbank effect, Phys. Rev. Lett. 121, 250401 (2018).
[4] Y.-H. Chan, Hong-Chen Jiang, and Y.-C. Chen, Plaquette valence bond state in spin-1/2 J1-J2 XY model on square lattice, Phys. Rev. B 107, 214402 (2023).
[5] C.-C. Chen, R. G. Escudero, J. Minář, B. Pasquiou, S. Bennetts, and F. Schreck, Continuous Bose–Einstein condensation, Nature 606, 683 (2022).









 首頁
首頁