【專欄】主成分分析及其在影像處理上的應用
作者 / 陳素雲研究員(本院統計科學研究所)、周芷妤博士後研究人員(國立臺灣大學健康數據 拓析統計研究所)

隨著大數據時代的到來,在許多研究領域與應用上往往面臨大量高維度數據的分析。大量數據提供更多的訊息量,但其中可能伴隨著一些雜訊,或不可信賴的異常值和離群值,因而導致分析偏誤,進而影響到最終對分析結果的決策及判斷。除此之外,大數據也增加了分析上的計算成本、複雜度,造成運算上的負擔,因此,需要找到適當的分析方法及工具,將數據「化繁為簡、去蕪存菁」。這不僅意味著除去不必要的訊息,同時盡可能地保留原始數據中的有用訊息,以減輕分析過程中的時間和成本負擔,實現對數據更全面了解的目標。
在統計學及機器學習領域中,主成分分析(Principal Component Analysis, PCA)即為一種常用的降低數據維度的手法。主成分分析由英國數學家卡爾 ‧ 皮爾森(Karl Pearson)於 1901 年提出1,是一種歷史悠久且相對容易運用的降維度(dimension reduction)、去關聯性的方法,至今在數據分析領域中仍被廣泛地應用。主成分分析是一種非監督式學習(unsupervised learning),其主要的核心概念是用最少的維度來呈現原本高維度數據的訊息:將原本 p 維的特徵(features)以 k 維的線性組合來表達(其中k < p),藉由主成分(Principal Components)找到的 k 維新特徵,其能夠捕捉原本 p 維數據中的大部分的特性來解釋數據。換言之,希望能夠在盡量保有原始數據訊息的情況下,以更精簡化的形式來呈現原始數據。
PCA 原理
主成分分析的目的是將資料進行降維,並找出最能夠解釋資料的方向:找到一個或一個以上的投影軸(向量),將資料點線性投影到這個(些)軸上後,使得資料有最大的變異量,而且新特徵彼此之間線性不相關。
假設有 n 個樣本點,![]() xi ∈ Rp,透過主成分分析將資料點投影到新座標軸的做法為:
xi ∈ Rp,透過主成分分析將資料點投影到新座標軸的做法為:
1. 先將資料中心移至原點(亦即使平均數為 0),在此不妨假設平均數皆已為零。
2. 找到新的座標軸,使得投影後的資料有最大的變異量。這個問題可以透過解共變異數矩陣(covariance matrix)S 的特徵值分解(eigenvalue decomposition)得到:
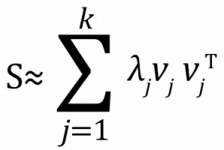
vj⊤vj = 1 及 vl⊤vj = 0,l ≠ j。
這裡的 vj ∈ Rp 對應的是共變異數矩陣 S 的第 j 個特徵向量(eigenvector),λj 即為第 j 個最大的特徵值(eigenvalue)。舉例來說,![]() 則為原資料點投影到 v1 上的新座標,這些投影後的資料點在 v1 這個方向有最大的變異量。因此,主成分分析藉由特徵值分解來找 k 個新的座標軸,找到的 k 個特徵向量也就是資料的主成分,而且 k 個主成分彼此之間為正交(orthogonal),資料投影後的變異程度則是由特徵值來描述。以一個例子來說明,令特徵向量矩陣為V = [ v1 v2 … vk ] ∈ Rp×k,其對應的特徵值為 λ1 ≥ λ2 ≥ … ≥ λk > 0,將原資料點 x1 投影到新的座標空間上得到的新特徵為 z1=[z11 z12 ⋯ z1k ]⊤ ∈ Rk:
則為原資料點投影到 v1 上的新座標,這些投影後的資料點在 v1 這個方向有最大的變異量。因此,主成分分析藉由特徵值分解來找 k 個新的座標軸,找到的 k 個特徵向量也就是資料的主成分,而且 k 個主成分彼此之間為正交(orthogonal),資料投影後的變異程度則是由特徵值來描述。以一個例子來說明,令特徵向量矩陣為V = [ v1 v2 … vk ] ∈ Rp×k,其對應的特徵值為 λ1 ≥ λ2 ≥ … ≥ λk > 0,將原資料點 x1 投影到新的座標空間上得到的新特徵為 z1=[z11 z12 ⋯ z1k ]⊤ ∈ Rk:
其中 vj⊤vj = 1 及 vl⊤vj = 0,l ≠ j。以此類推,我們可以將 n 個樣本點投影後得到[z1 z2 ⋯ zn]k×n=[v1 v2 ⋯ vk]⊤ [x1 x2 ⋯ xn]p×n,其中 zi=[zi1 zi2 ⋯ zik ]⊤。我們稱 vj 為第 j 個主成分,zi 則被稱作主成分分數(principal component scores)。我們有以下性質:
(i) ![]() ,亦即第 j 個新特徵的變異數即為 λj;兩兩特徵之間彼此不相關。
,亦即第 j 個新特徵的變異數即為 λj;兩兩特徵之間彼此不相關。
(ii) ![]() ,亦即原特徵的變異數總和(共變異數矩陣的 trace)即為特徵值的總和。
,亦即原特徵的變異數總和(共變異數矩陣的 trace)即為特徵值的總和。
(iii) 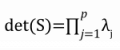 ,亦即所有特徵值的乘積即為共變異數矩陣的行列式。
,亦即所有特徵值的乘積即為共變異數矩陣的行列式。
.PCA 的歸納總結
1. 精簡化(parsimony):用較少的主成分來取代原本的高維度特徵。
2. 代表性(representation):主成分保有原本特徵的訊息。
3. 去相關(decorrelation):主成分分數(即新特徵)彼此之間無線性相關。
穩健主成分分析方法
雖然主成分分析相當普及且已被廣泛地應用於數據分析上,但是當資料中有離群值(outliers)的存在,或我們稱之為資料受到汙染(contaminated)時,主成分分析的結果容易產生有偏估計(biased estimation)。因此,許多具有穩健性(robustness)的主成分分析方法已被提出來克服資料中有離群值存在的情況,使得估計的結果更加穩健、可信。面對極端值存在的情況,一種常見的策略是根據穩健散點矩陣估計(robust scatter matrix estimator)來執行特徵值分解。陳素雲研究員及其合作者(台大的洪弘教授及日本統計數理研究所的江口真透教授)在 2022 年提出了 Robust Semiparametric PCA[2]2,此方法是基於半參數理論(Semiparametric Theory)與 robust scatter estimator 發展出來的一種具有穩健性的主成分分析方法。
.Robust Semiparametric PCA(SPPCA)
考慮一個半參數模型(semiparametric model):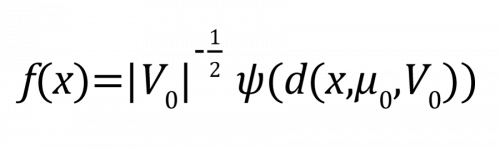
其中d(x,μ0,V0) = (x – μ0)⊤V0-1(x-μ0)。(μ0,V0) 為感興趣的參數(欲估計的參數),ψ(・) 為無窮多維的干擾參數(infinite-dimensional nuisance parameter),干擾參數為不感興趣,但必須考慮的參數。半參數理論在不需指派 ψ(・) 的形式下,確保了對參數(μ0,V0)估計式的建構,因此,根據半參數理論, SPPCA 提出透過以下估計式對參數(μ0,V0)做估計:
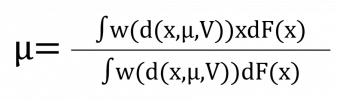
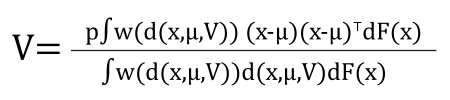
其中 w(・) 為權重函數(weight function),F(x) 為f(x) 的累積機率函數(cdf)。上述 SPPCA 對 V0 的估計式可以重新整理成以下形式:
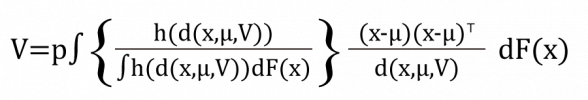
其中 h(u)=w(u)u。SPPCA 透過大括號中的部分給予每個資料點不同的權重,納入 d(x,μ,V) 的訊息及選擇適合的權重函數 w(・) 後,給予極端值較小的權重,降低極端值對估計結果的影響程度,以達到穩健的估計結果。為了達到這樣的目的,SPPCA 對於權重函數 w(・) 的選擇須滿足以下兩個條件:
(1) ![]()
(2) ![]()
條件(1) 確保 SPPCA 的影響函數(influence functions)的長度(norm)是有界的;條件(2) 則保證在有離群值的情況下,SPPCA 的估計結果具有穩健性。
PCA 於影像處理上的應用
主成分分析的應用相當多元,在影像分析上可以用於
1. 降維:降低影像數據的維度,進而減少數據的複雜度,但同時保留原本數據中主要的特徵/特性。
2. 特徵提取(feature extraction):識別及提取影像中最具有代表性的特徵,助於後續分析和辨識影像的進行。
3. 降噪(denoise):去除影像中不必要的雜訊,保留影像中相對重要的細節,提高影像的質量,讓影像更加清晰。
接下來將介紹主成分分析於人臉辨識的應用,透過主成分分析方法將影像中的臉部特徵抓取出來,減少誤判影像的機會,提高臉部辨識的成功率。
.Olivetti Faces Dataset
Olivetti 資料集是一組從 1992 年 4 月至 1994 年 4 月於 AT&T 劍橋實驗室拍攝的臉部影像。資料集包含 400 張對於不同的 40 個人所拍攝的臉部影像,每個人各拍攝 10 張,這些影像是在不同時間、光線、臉部表情(微笑/不微笑、睜眼/閉眼)及臉部細節(戴眼鏡/不戴眼鏡)之下拍攝,圖一展示 16 張隨機選取的影像。每一張影像皆被轉成灰階(數值界於 0 至 255 )、大小為 64×64 的臉部影像矩陣。

▲圖一:Olivetti faces。
圖二為透過主成分分析的結果,第一行到第四行呈現低維度影像重建(low-rank reconstructions)的結果,第五行到第八行呈現 PCA 提取的臉部特徵(eigenfaces),或稱為基底空間(leading basis functions)。在這個分析中,以維度 126 的臉部特徵矩陣(其中包含 mean face)來對原本維度 4096 的臉部影像矩陣進行低維度影像重建。

▲圖二:PCA 的低維度影像重建(low-rank reconstructions)及基底空間(leading basis functions)。
接下來呈現影像中存在離群值的分析結果,將文獻上的兩種穩健主成分分析方法應用於 Olivetti 資料集中:(1)2011 年由 Candès 等學者所提出的 robust PCA3 及(2)前述介紹的 Robust Semiparametric PCA3。此分析將 20 張隨機旋轉的招財貓影像(圖三展示 16 張隨機選取的影像)作為離群值加入 Olivetti 資料集中,因此,資料中含有 420 張影像。
▲圖三: Outliers。
由圖四的結果顯示,Candès 等學者所提出的 robust PCA 找出的特徵受到了離群值的污染,基底空間圖像中明顯可以看到招財貓的影像,從影像重建的結果可以看出臉部表情有一點模糊、輪廓不夠清楚,並且失去了一些細節。我們提出的 Robust Semiparametric PCA 在極端值存在的情況下,能夠較為不受到離群值的影響,成功識別出主要的特徵(見圖五),影像重建的結果更接近真實情況(即圖一),與 Candès 等學者所提出 robust PCA,相比具有更精細的臉部特徵。

▲圖四:Candès 等學者所提出的robust PCA 的低維度影像重建(low-rank reconstructions)及基底空間(leading basis functions)。

▲圖五:我們的 Robust Semiparametric PCA 的低維度影像重建(low-rank reconstructions)及基底空間(leading basis functions)。
總結
本文介紹了主成分分析的原理,包括如何找到最能夠解釋數據變異的主成分,以及如何降低數據維度。此外,還討論了穩健性主成分分析方法及其在影像降維方面的應用,特別是介紹了一種稱為 Robust Semiparametric PCA 的方法,以應對數據中的離群值。在這之中,半參數理論(Semiparametric Theory)是統計學中一個重要的理論框架,它整合了參數方法和非參數方法的優點,使其應用於一些複雜模型的推論時,擁有更大的靈活性。這種半參數方法使統計學家能夠更靈活地應對複雜的數據情境,進而做出更為可靠的推斷和預測。
1 Pearson, K. (1901). On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 2(11), 559-572.
2 Hung, H., Huang, S. Y., and Eguchi, S. (2022). Robust self-tuning semiparametric PCA for contaminated elliptical distribution. IEEE Transactions on Signal Processing, 70, 5885-5897.
3 Candès, E. J., Li, X., Ma, Y., and Wright, J. (2011). Robust principal component analysis? Journal of the ACM, 58(3), 1-37.









 首頁
首頁