中央研究院 Logo

物理學吸引人的地方在於，把兩個看似不同的現象找出底層的共同原理來解釋，例如：月亮繞著地球轉和物體會往地上掉，都遵守相同的原理與受到同樣的地心引力。在物理學家的眼中，肥皂泡沫與上皮細胞有分享一些共同原理，在這篇文章我就講述這兩個看似很不同的系統一些令人驚訝的發現。

在中研院附近工作的人，可能都看過中國信託金融園區旁，三重世貿公園的一個大型雕塑 (圖一a)。該雕塑的結構叫做「Weaire-Phelan structure」，也是 2008年北京奧運水立方建築上的造型結構，這個結構在超過一個世紀前，由Lord Kelvin解出。

在1887年，Lord Kelvin 提出了一個問題：「如何用體積一樣的小單位填滿空間，會有最小的表面積？」會激發這個問題是因為泡泡有表面張力，系統要往降低能量型態演進，就要減少表面面積，所以一個單獨泡泡的形狀是圓球，這是最小表面積的形狀。

當多個泡泡碰在一起，形成泡沫時，它們的交界會滿足 Plateau’s law，三個邊的交界角度會是 120 度，如果是四個邊交界角度會是 109.47 度，當滿足這個規律時，結構就會是最小表面積（這個證明在1976 年由 Jean Taylor 提出[1]）。

所以如果體積一樣的小單位排列在一起時，要有最小表面積，如果是單層平片結構，會是六方堆積 (圖一b)，而如果是在三維排列， Kelvin 猜測最佳解是bitruncated cubic honeycomb，又稱作「Kelvin structure」，但是超過一個世紀這個猜測並沒有被證明，也沒有找出更好的解。

1993 年由愛爾蘭物理學家 Denis Weaire 和他的學生 Robert Phelan 透過電腦模擬找到一個比 Kelvin structure 更小表面積的結構，只是在這個結構由兩個不同的小單位組成 [2]。實驗上，一直到 2011 年做出合適邊界條件才實驗上觀察到 Weaire-Phelan structure [3]，否則平片的邊界條件會偏好 Kelvin 結構。

圖一 (a) 世貿公園裡的大型雕塑。(b) 均一大小泡沫在二維平面上排列成六方堆積。(c)均一大小泡沫在三維排列成 Kelvin 結構(圖來自於 Physics of Foam [4]。)

泡沫的組成很簡單，有氣體、液體和界面活性劑，如果我們考慮它的物理性質，直覺上會覺得泡沫性質會接近液體，因為組成泡沫物質都有相當的流動性。研究物質的流動性質的科學稱為流變學，測量方法就是對於要研究的物質，我們給一定的應力，如果物質是固體，物質的反應是形變，呈現出像彈簧的彈性係數；如果物質是液體，物質會有流動，呈現出像液體的黏滯係數。

生活中許多物質就同時具有這兩種性質，甚至會隨著應力大小有不同的反應，泡沫就是這樣的物質。它可以像固體，所以像刮鬍的泡沫噴出來時，它們能維持形狀，不會因重力滴下來(圖二)，但是在用刮鬍刀去抹時（相當於給予應力），這個泡沫會流動，會均勻地抹在臉上。而泡沫流變性質之豐富比固體、液體這樣的變化還要豐富。

生物系統中的表皮細胞和泡沫有很多相似的結構，很早生物學家就觀察到有些細胞排列呈現六方堆積，例如：水晶體裡面的纖維細胞排列或者果蠅翅膀上的上皮組織，所以是否上皮細胞排列時也需要符合降低表面張力的規則？

只是上皮細胞的表面張力比泡泡複雜，泡泡的表面張力到處都一樣，但是上皮細胞有極性，分成頂面，側面與底面，所以在不同面可以有不同的表面張力，這些表面張力可能是來自於細胞膜上的黏著分子，也可能來自於與黏著分子相連細胞內部的小肌肉(肌動凝蛋白束 actomyosin)，所以張力可以是吸引力也可以是排斥力，甚至在三個細胞交界的點也可以有不一樣的能量，考慮在不同點、線、面都有不同能量的模型，叫做「vertex model (頂點模型)」（圖三a）。

在2008年，Sascha Hilgenfeldt 成功地用簡單版的vertex model預測出果蠅眼睛裡面小眼細胞的排列（圖三b），並且他與生物學家合作，生物學家改變小眼細胞內一些細胞邊邊面的張力，小眼細胞內部排列就改變，而Sasha的模型也都能預測這些變化（圖三c） [5]。
2018 年時，西班牙科學家Javier Buceta用vertex model發現了上皮細胞如果在曲面上排列，要降低表面的能量，會形成的一種新形狀，在幾何課本從來沒探討過的新形狀，它們將這個形狀命名為scutoid [6]。過去上皮細胞在曲面上排列時，大家都會認為頂面與底面的形狀是一樣的，例如：都是六邊形或者是五邊形，Javier 的模擬顯示可以一面是六邊形、另一面是五邊形，所以旁邊的面不會是完全的平面，而會多了一個三角形的面，講六邊型的兩個頂點縮為一個，再與五邊形的另一面相連，而這個形狀上下翻轉，就能完美的嵌合在一起（圖三d）。而除了在電腦模擬中發現了這個新形狀，他們也做實驗，在果蠅的唾腺細胞裡找到這個新形狀。這個新形狀其實都存在我們身體裡，只是我們一直不知道。

圖三(a)上皮細胞有三個面的張力，圖來自於[7]。(b)上圖是野生型果蠅小眼內細胞的排列，下圖是理論計算出來的排列，與照片吻合。(c)上圖是突變的細胞，所以排列與野生型不同，下圖是考慮突變後造成張力的變化，預測出來的型態，與觀察一致。(d) 上圖是曲面上排列上皮細胞，同一個細胞在內側曲面與外側曲面的形狀會不一致，這時的形狀就是如下圖的 scutoid，這個 scutoid 能互相堆疊。

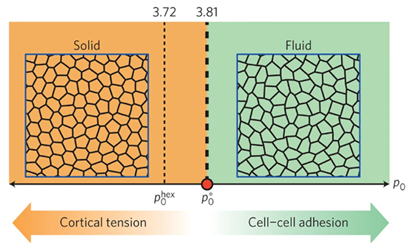
泡沫有違反直覺的流變性質，上皮細胞的流變性質為何？許多上皮細胞流變性質研究都著重在上皮細胞密度改變時流變形質的變化。2015 年在雪城大學物理系教授 Lisa Manning 提出一個與密度無關的轉變，只要考慮一個很簡單的參數為形狀指數 shape index，定義是周長除以根號面積  所以正六邊形p = 3.72，正五邊形是p=3.81，所以當一個系統平均的p大於3.81 時，上皮組織的性質就比較接近液體，小於3.81時就比較接近固體 [8]。

上皮細胞竟然能有像固體的性質。在古典物理中固體性質的一大特色就是它能傳遞機械波，古典機械波的震盪是來自於 . 其中 k 是彈性係數，x是位移，m 是粒子的質量， 是位移對於時間的二次微分，也就是加速度。這個數學關係式的解會有正弦波形式。但是上皮細胞這個系統的尺度很小，它的高度只有十微米左右，在這個尺度，將遵守低雷諾係數的流力性質，不需要考慮慣性的影響。

沒有慣性就沒有加速度，理論上就應該不會有機械波，但是 2012 年另一組西班牙科學家 Javier Trepat 實驗室觀察到當上皮細胞集體主動爬行擴張時，細胞組織會呈現出密度波，再更進一部探討這個密度波傳遞的本質時，他們發現是透過肌動凝蛋白束傳遞的機械波，他們測量細胞爬行時產生的應力和上皮組織產生的形變，這兩個量在時間與空間上都會來回震盪，兩個量變化有同相，此外因為當肌凝蛋白的收縮力被關掉時，就不會有機械波了[9]。到這篇文章為止，大家都認為在生物系統觀察到的波是化學波，為什麼在上皮細胞層片裡這些化學波還要被轉成機械波？但是為什麼生物系統需要機械波？它的生物功能是什麼?

要了解這個謎題，必須在生物體做實驗才容易找到機械波的生物功能。在2017年，本院細胞與個體生物學研究所陳振輝副研究員為了瞭解再生的一個謎團：斑馬魚尾巴不管切多少，最後長回來的時間是一樣的，所以切越多，再生速度越快，他想了解斑馬魚如何感測失去多少尾巴，實驗室觀察切掉尾巴後上皮細胞的行為。

發現上皮細胞快速爬行去包覆傷口時，會往身體方向傳遞一個密度波，而切越多，這個波傳遞越遠(圖五a)。為了更進一步瞭解這個波的性質，他找了我實驗室共同合作，我們做實驗證明這個波傳遞的本質也是機械波—在魚尾巴上面做雙狹縫干涉實驗，發現波會干涉(圖五b)，波傳遞的速度與斑馬魚尾巴張力成正比(圖五c)，最後建立機械波模型，成功的解釋波的行為。

我們也發現大部分細胞增生都發生在波傳遞的範圍中，所以切越多尾巴，波傳遞越遠，越多細胞增生(圖五d)，解釋了再生速度會增加 [10]，而我們實驗室最近把尾巴切的很短，剩下的長度低於波傳遞的距離，這樣子魚尾巴就不會同時間長回來了(圖五e)。我們這個研究除了解釋了再生的其中一個謎團，也顯示生物體會傳遞物理訊號，而不是單純的化學訊號，來執行生物功能。

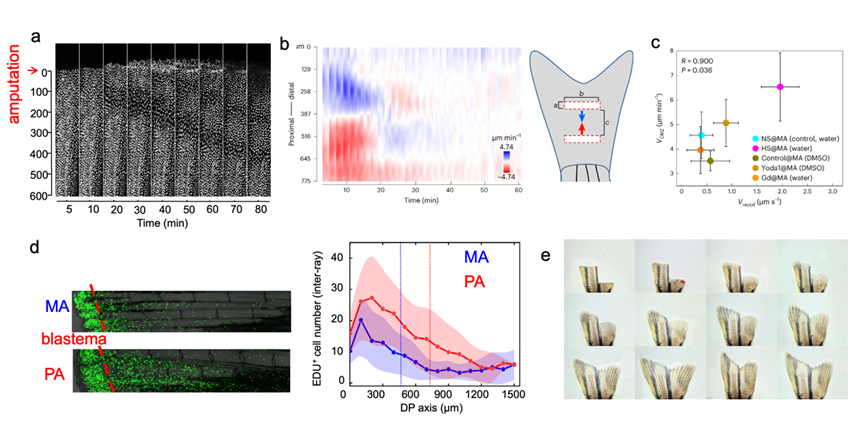
圖五 (a)魚尾巴上皮細胞的集體遷移，圖中的亮點是細胞核，細胞往傷口方向跑（上方），而一個波往下方傳遞。(b)魚尾巴畫兩個傷口，會形成兩個方向相反的波，互撞之後，會干涉。(c) Y軸是測量波速，X軸是測量魚尾巴張力的後座速度，兩者呈正向線性關係。(d)兩點顯示將會進行細胞分裂的細胞，他們發聲的位置大多在波傳遞範圍之內。前面的圖都是來自於[10]。(e)將右側尾巴撿到幾乎靠近於身體，波傳遞距離大於剩下的部位。魚尾再生就不會同時回來。此圖為鄭愷修(林耿慧實驗室)的工作。

在上個世紀，物理學家在了解非生命物質獲取很大的成功，我們也了解生命物質中沒有額外的生命作用力(vital force)，生命體內部是靠已知的作用力，如：氫鍵、凡德瓦力、熵在運作，裡面組成物質有很精密的協調，來對抗生命體內熵的增加，執行生命運行的步驟。在這些精密的協調一定隱藏了許多物理原則，或者可以利用物理語言來了解這些生命現象，例如：在這篇文章裡舉的幾個例子。這都是二十一世紀物理學家可以發現的新物理，期待在二十一世紀，物理學家可以與生物學家有更密切的合作，我們可以描述生命物質就像物理學家能描述非生命物質一樣，這樣的了解將有助於我們更近一步操控生命現象，解決疾病，甚至了解生命的起源。

參考資料：

1.     Taylor JE, editor The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces1976.

2.     Weaire D, Phelan R. A counter-example to Kelvin's conjecture on minimal surfaces. Philosophical Magazine Letters. 1994;69(2):107-10. doi: 10.1080/09500839408241577.

3.     Gabbrielli R, Meagher AJ, Weaire D, Brakke KA, Hutzler S. An experimental realization of the Weaire–Phelan structure in monodisperse liquid foam. Philosophical Magazine Letters. 2012;92(1):1-6. doi: 10.1080/09500839.2011.645898.

4.     Weaire D, Hutzler S. The Physics of Foams: Oxford University Press; 2000. Available from: https://doi.org/10.1093/oso/9780198505518.001.0001.

5.     Hilgenfeldt S, Erisken S, Carthew RW. Physical modeling of cell geometric order in an epithelial tissue. Proceedings of the National Academy of Sciences. 2008;105(3):907-11. doi: doi:10.1073/pnas.0711077105.

6.     Gómez-Gálvez P, Vicente-Munuera P, Tagua A, Forja C, Castro AM, Letrán M, et al. Scutoids are a geometrical solution to three-dimensional packing of epithelia. Nature Communications. 2018;9(1):2960. doi: 10.1038/s41467-018-05376-1.

7.     Hannezo E, Prost J, Joanny J-F. Theory of epithelial sheet morphology in three dimensions. Proceedings of the National Academy of Sciences. 2014;111(1):27-32. doi: doi:10.1073/pnas.1312076111.

8.     Bi D, Lopez JH, Schwarz JM, Manning ML. A density-independent rigidity transition in biological tissues. Nature Physics. 2015;11(12):1074-9. doi: 10.1038/nphys3471.

9.     Serra-Picamal X, Conte V, Vincent R, Anon E, Tambe DT, Bazellieres E, et al. Mechanical waves during tissue expansion. Nature Physics. 2012;8(8):628-34. doi: 10.1038/nphys2355.

10.   De Leon MP, Wen F-L, Paylaga GJ, Wang Y-T, Roan H-Y, Wang C-H, et al. Mechanical waves identify the amputation position during wound healing in the amputated zebrafish tailfin. Nature Physics. 2023;19(9):1362-70. doi: 10.1038/s41567-023-02103-6.